Extended isolation forest

Link to original paper	Authors	Publication year
Here	Sahand Hariri, Matias Carrasco Kind, Robert J. Brunner	2018

The idea in 2 lines

The authors propose to improve the expressibility of Isolation Forest trees by using random hyperplanes instead of standard constant splits.

Some context before reading the paper

The standard Isolation forest (IF) algorithm is an unsupervised anomaly detection algorithm that relies on how easy it is to separate this point from all others using random splits to caracterize the likeliness that a given data point is an anomaly. relies on.

Other algorithms usually rely on density (e.g. Local Outlier Factor or DBSCAN), which entails additional computations to measure distances between data points.

The IF algorithm will train many simple trees, each of which will be able to isolate data points using a different number of splits. Figure 1 and 2 depict how a single tree isolates two different points. An anomaly is expected to be easy to isolate, i.e. to require few splits (6 splits on fig. 1). On the other hand, a “regular” point will be harder to isolate (12 splits on fig. 2).

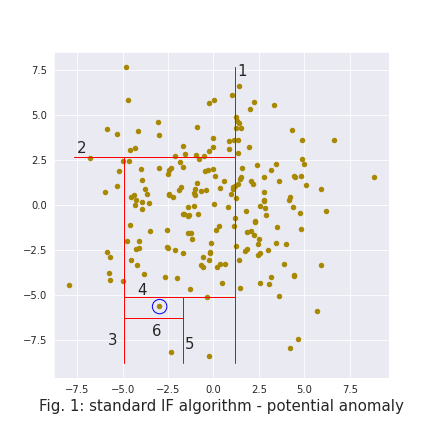
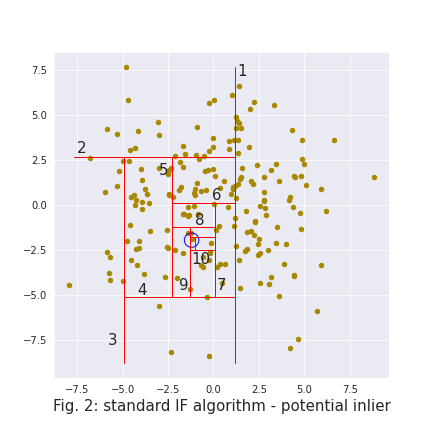
This random split-based approach greatly reduces the computation complexity, but also induces artifacts in the model’s decision boundaries. As can be seen in figure 3, the splits create a vertical & horizontal bias.

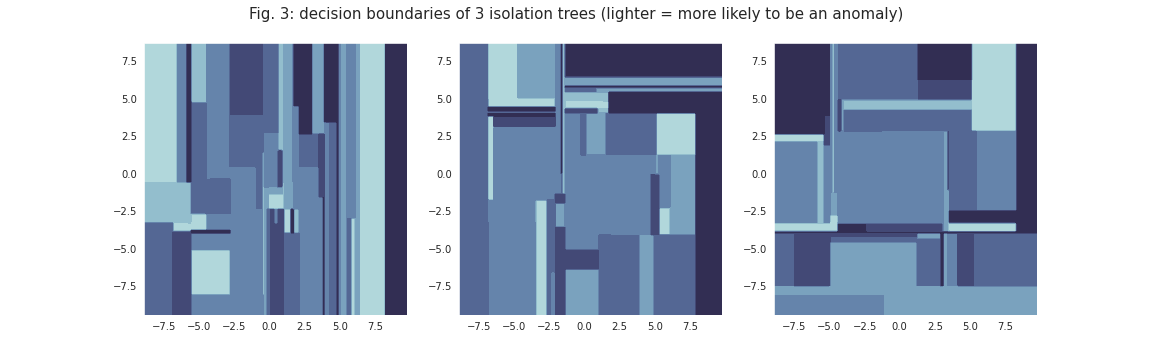
These individual biases are conserved when the trees are combined to form the final classifier, as can be seen in figure 4.

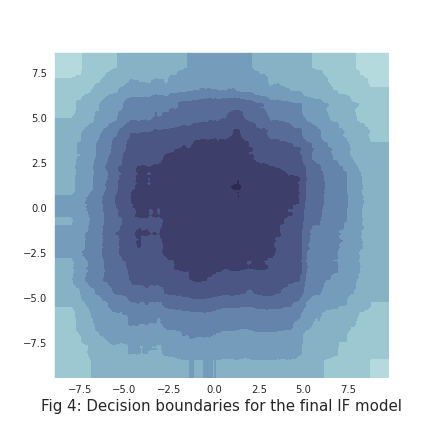
The purpose of the Extended Isolation Forest presented in the paper is to handle this issue.

Ready to learn more? Dive in!